Pref

程序 = 数据结构 + 算法

数据结构和算法的学习整理，部分用英文书写。

Data Structure

Logical Structure

1.集合结构：集合中没有相同的数据元素。

2.线性结构：元素之间是「一对一」关系，数组、链表、栈、队列、哈希表。

3.树形结构：元素之间是「一对多」层次关系，二叉树、字典树。

4.图形结构：元素之间是「多对多」关系，无向图、有向图、连通图。

Physical Structure

1.顺序存储结构（Sequential Storage）：连续

2.链式存储结构（Linked Storage）：连续/不连续

Algorithm

五个特性：输入、输出、有穷、确定、可行性

比较算法优劣的两种方法：

事后统计：各编写一个可执行程序，执行后记录下各自的运行时间和占用空间，挑选出最好的算法。(工作量太大)
预先估算：算法设计出来后，估算出算法的运行时间和占用空间，比较估算值，从中挑选。（常用）

Time Complexity

在问题的输入规模为 n 的条件下，算法运行要花费的时间，记作 T(n) = O(f(n))
O 是一种渐进符号，T(n) 称作算法的渐进（Asymptotic）时间复杂度。
「基本操作次数」作为时间复杂度的度量标准。

求解时间复杂度：

找出算法中的基本语句：执行次数最多的语句就是基本语句，通常是最内层循环的循环体部分。
计算基本语句执行次数的数量级：保证函数中的最高次幂正确即可。
用大 O 表示法表示时间复杂度：将数量级放入 O 渐进上界符号。

常用数量级：

常数 O(1)
线性 O(n)
平方 O(n²)
指数 O(2^n)
阶乘 O(n!)
对数 O(log₂n)
线性对数 O(nlog₂n)

常见时间复杂度关系：

O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2^n) < O(n!) < O(n^n)

递归算法的时间复杂度 = 每次递归的时间复杂度 * 递归次数
递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度

求 x 的 n 次方的递归算法复杂度分析：

一个 for 循环，时间复杂度为 O(n)。

int function1(int x, int n) {
    int result = 1;  // 注意 任何数的0次方等于1
    for (int i = 0; i < n; i++) {
        result = result * x;
    }
    return result;
}

递归算法 1，每次 n-1，递归了 n 次是 O(n)，每次进行了一个乘法操作是 O(1)，故时间复杂度是 n × 1 = O(n)。

int function2(int x, int n) {
    if (n == 0) {
        return 1; // return 1 同样是因为0次方是等于1的
    }
    return function2(x, n - 1) * x;
}

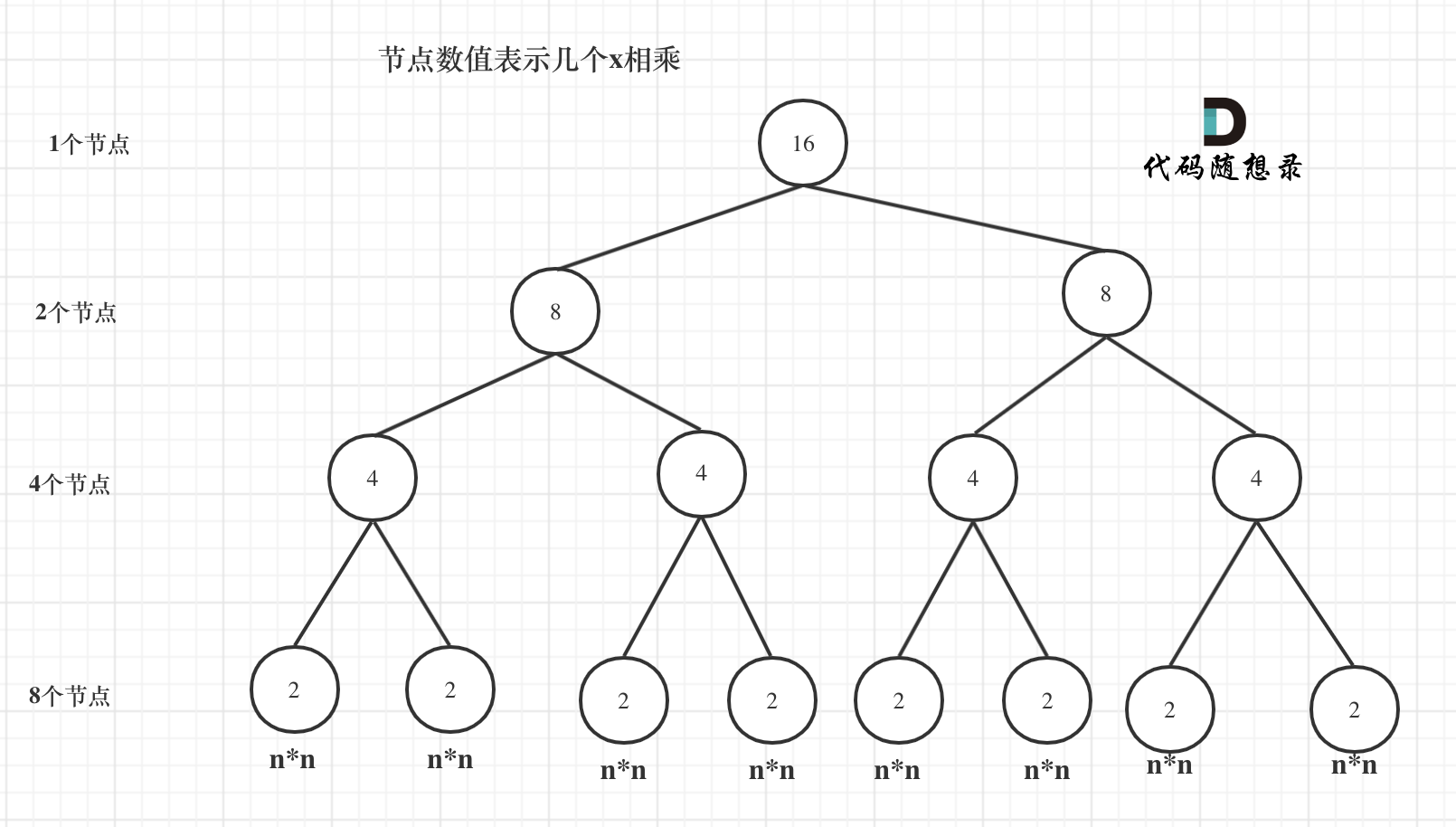
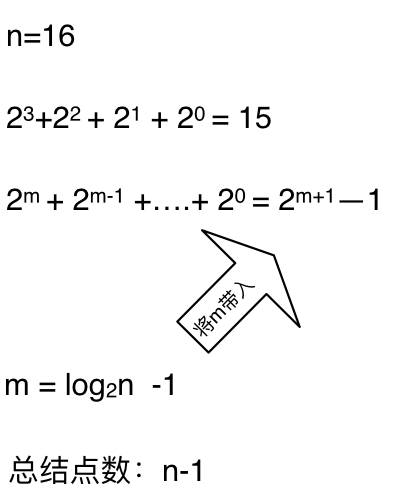
递归算法 2，把递归抽象出一棵满二叉树，每个节点代表着一次递归并进行了一次相乘操作，所以递归数即节点数。其节点数是 2^3 + 2^2 + 2^1 + 2^0 = 15（等比数列求和）。

求 x 的 n 次方，m 为深度。时间复杂度还是 O(n)。

int function3(int x, int n) {
    if (n == 0) {
        return 1;
    }
    if (n % 2 == 1) {
        return function3(x, n / 2) * function3(x, n / 2)*x;
    }
    return function3(x, n / 2) * function3(x, n / 2);
}

递归算法 3，只有一个递归调用，且每次都是 n/2，即调用了 log₂n 次，每次递归都做一次乘法操作，常数项忽略，故时间复杂度是 O(logn)。

int function4(int x, int n) {
    if (n == 0) {
        return 1;
    }
    int t = function4(x, n / 2);// 这里相对于function3，是把这个递归操作抽取出来
    if (n % 2 == 1) {
        return t * t * x;
    }
    return t * t;
}

求斐波那契数列的性能分析：

非递归，时间复杂度 O(n)，空间复杂度 O(1)。

int main() {
    int n1 = 0, n2 = 1, n3, i, n; //n 为打印数
    cin >> n;
    if (n <= 1) cout << n1 << endl;
    if (n == 2) cout << n1 << " " << n2 <<endl;
    if (n > 2) {
        cout << n1 << " " << n2;
        for (i = 3; i <= n; ++i) {
            n3 = n1 + n2;
            cout << " " << n3;
            n1 = n2;
            n2 = n3;
        }
    }
    return 0;
}

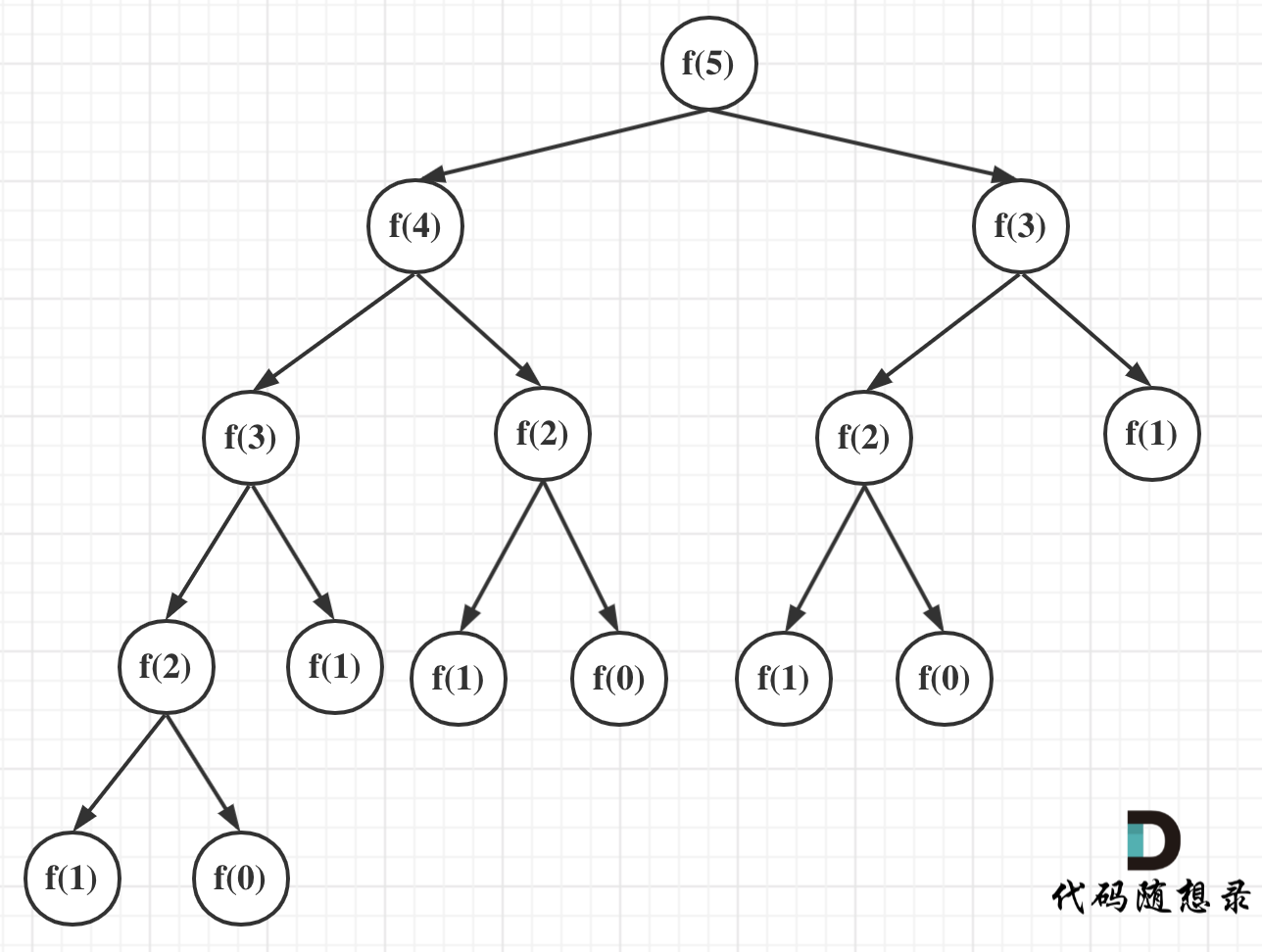
递归算法，每次递归都是 O(1)，抽象出一棵递归树，递归次数最多为 2^n-1 个节点数（n 为深度），故时间复杂度 O(2^n)；每次递归的空间复杂度是 O(1)，调用栈深度为 n，故空间复杂度 O(n)。

int fibonacci(int i) {
       if(i <= 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i-1) + fibonacci(i-2);
}

递归算法，每次递归的时候 n-1，即只是递归了 n 次，时间复杂度 O(n)，空间复杂度 O(n)。

//fibonacci(1, 1, n);
int fibonacci(int first, int second, int n) {
    if (n <= 0)
        return 0;
    if (n < 3)
        return 1;
    else if (n == 3)
        return first + second;
    else
        return fibonacci(second, first + second, n - 1);
}

使用递归算法并不一定是性能最优，但能简化代码。

Space Complexity

在问题的输入规模为 n 的条件下，算法所占用的空间大小，记作为 S(n)。
「算法的辅助空间」作为空间复杂度的度量标准。

空间复杂度更容易计算，主要包括
「局部变量（算法范围内定义的变量）所占用的存储空间」
「系统为实现递归（如果算法是递归的话）所使用的堆栈空间」

常见空间复杂度关系：

O(1) < O(logn) < O(n) < O(n²) < O(2^n)

Array

数组：线性表顺序存储结构。使用一组连续的内存空间，存储一组相同类型的数据，可随机访问。

寻址公式：下标 i 对应的数据元素地址 = 数据首地址 + i * 单个数据元素所占内存大小

访问元素：

def value(nums, i):
    if 0 <= i <= len(nums) - 1:
        print(nums[i])

arr = [0, 5, 2, 3, 7, 1, 6]
value(arr, 3)

查找元素：（线性查找）

# 从数组 nums 中查找值 val 第一次出现的位置
def find(nums, val):
    for i in range(len(nums)):
        if nums[i] == val:
            return i
    return -1

arr = [0, 5, 3, 7]
print(find(arr, 7))

插入元素：

# Python 中 list 封装了尾部插入操作，直接调用 append 方法，该方法当数组满了，会开辟新空间插入。
arr = [0, 5, 3, 7]
val = 4
arr.append(val)
print(arr)

# Python 中 list 封装了中间插入操作，直接调用 insert 方法即可。
arr = [0, 5, 3, 7]
i, val = 2, 4
arr.insert(i, val)
print(arr)

改变元素：

def change(nums, i, val):
    if 0 <= i <= len(nums) - 1:
        nums[i] = val

arr = [0, 5, 3, 7]
i, val = 2, 4
change(arr, i, val)
print(arr)

删除元素：

# Python 中的 list 直接封装了删除数组尾部元素的操作，只需要调用 pop 方法即可。pop()：根据索引值删除元素
arr = [0, 5, 3, 7]
arr.pop()
print(arr)

# Python 中的 list 直接封装了删除数组中间元素的操作，只需要以下标作为参数调用 pop 方法即可。
arr = [0, 5, 3, 7]
i = 1
arr.pop(i)
print(arr)

# 基于条件删除元素：要求删除满足某条件的元素。删除多个元素涉及到多次移动元素操作，将其转变为一趟移动元素，时间复杂度降为 O(n)。remove()：根据元素值进行删除
arr = [0, 5, 2, 3, 7, 1, 6]
i = 3
arr.remove(5)
print(arr)